Modelling the course of infectious diseases within a population provides a powerful approach for both forecasting and retrospectively understanding disease transmission. Such models allow us to unpick previous infections by optimising those model parameters which represent the rates of infection, recovery, death etc.

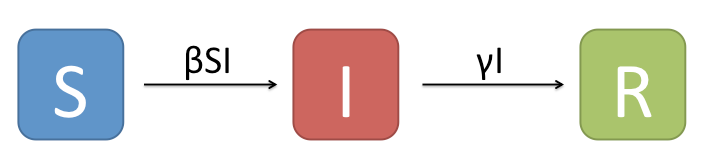
One classic method for modelling disease transmission within a population is the ‘SIR’ model, named for its three core sub-populations: Susceptible, Infected, and Resistant individuals. The core of this approach assumes a population in which individuals start as susceptible, have a chance to become infected, and then eventually gain resistance to the disease. More complex diseases can be modelled by adding different disease states or more complex rates, as discussed later.

Course of a Disease
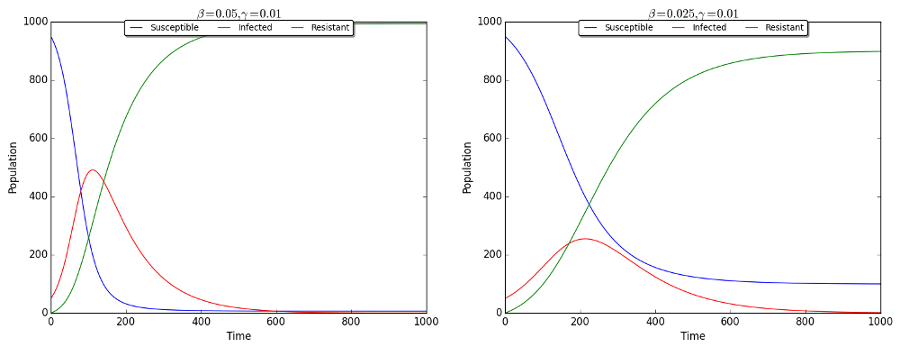
At time point zero, it is (usually) assumed that a population contains primarily susceptible individuals. Next, with each subsequent time point, a proportion (determined by rate beta ‘β’) of susceptible individuals become infected and a proportion (determined by rate gamma ‘γ’) of infected individuals become resistant. By tracking these sub-population sizes over time, we can plot the process of a disease and compare different initial model states, or different infection and recovery rates.

Extending the Model
The beauty of the SIR model lies in both its simplicity and expandability. Different diseases may be modelled simply by changing how the core model behaves.

For example, additional diseases states may be included to reflect that some infected individuals die rather than becoming resistant, or re-enter the suspectible population without gaining resistance. Variable rates can also be included, perhaps to mimic higher infection rates during winter time points. It is also possible to model the impact of multiple populations, whereby individuals move at a certain rate from population A to B, and vice versa. With each population potentially exhibiting its own SIR model.

Source Code
A Python version of the basic SIR model can be found on my github, feel free to extend and edit as you see fit.